Applied Regression Analysis

Interested in a free 25+ eBook on the 7 Wastes? Please DOWNLOAD HERE.

Sometime ago, I was able to do some work involving advanced statistics for a very complex process. This very large healthcare company was struggling with absenteeism issues — that is, the call center representatives would sometimes just not show up for work, or have other human resources issues. I wasn’t privy to those details, and I didn’t really care. But, I was concerned about the impact that absenteeism had on service level, which is defined as

Whenever you have a situation where you want to learn more about the impact of one or more variables has on another, then this business problem can be best understood with the Regression.

Regression Analysis

Regression deals with relationships between variables and also with Prediction: the ability to accurately predict behavior not only makes you more confident about decisions, but also implies an understanding of the processes at work. Regression in all its shapes and forms remains the central workhorse of social science research — economics, sociology, psychology, and is used in many areas of business and technology. It is central to techniques like conjoint and discrete-choice analysis; in fact, many pieces of the Google’s MapReduce technology (then do a CTRL-F on “Regression”) utilizes the regression — the way it is computational linguistics is to reduce noise in the data, in conjunction with Bayesian Statistics.

The problem above is a fairly simple one, but one that wasn’t fully understood in a quantitative way. But, with data to support people’s hunches that — yes, absenteeism does in fact impact service level — the company could have some solid evidence.

Regression Heuristics

• Predictor and Response: The predictor (x) is the variable we suspect has an influence on the response (y) variable. For our purposes, (x=absenteeism), and (y=service level).
• Intercept: In a regression equation, the intercept is the value of the response (y) when the predictor (x) equals zero.
• R^2: This is a mathematical term that describes how much of the variation in the data is explainable by the regression model. This value is between 0.0 and 1.0. The closer the R^2 value is to 1.0, then the more successful the regression model is in explaining variability in the data. The the R^2 is 0.0, then that means knowing (x) does not help us predict what (y) will be; in other words, it’s no better than chance or guessing.
• Slope: The slope of the regression line depicts the association between the (x,y) pair. In other words, in a regression the slope is the expected change in y for each unit change in x.

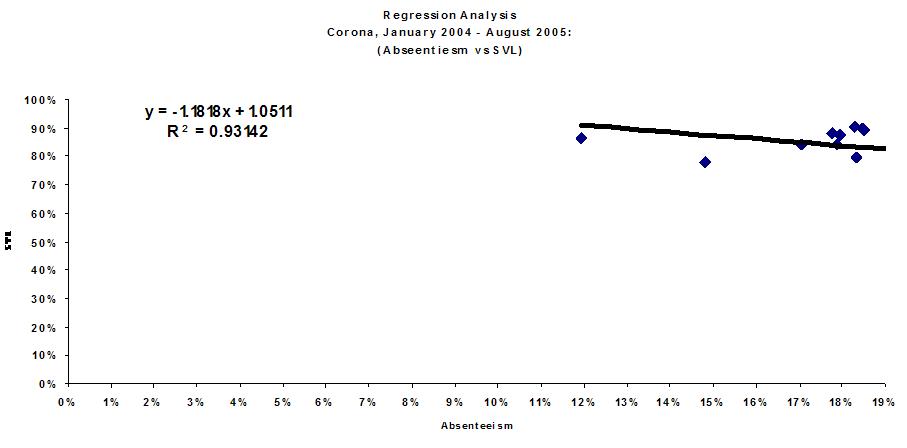
Above is the plot for the analysis of the absenteeism problem described. The data above allows us conclude the following:

• For a 1.18% decrease in absenteeism, we can probably expect a 1.05% increase in service level.
• There is a very strong relationship between service level and absenteeism as evidenced by the R^2 value of 0.93, which means that much of the data is explained by the regression model.

The data and analysis above supports the hunch that many people already had and, it’s pretty obvious in a lot of ways. So, why the analysis? Well, the company was a union shop and this topic was a very big union topic. The company now had hard data to show the union during their labor negotiations that, yes, absenteeism impacts the company and the customer in a very specific way. This data was used to leverage the negotiation process in favor of the company. Without the data, negotiating this piece would probably be much more difficult and may not have gone in favor of the company.

Conclusion

Regression is the workhorse of many important business-type analysis. I’ve learned during my short career that it’s not used nearly as much as it ought to be. Later, I’ll show how Regression is used in computational linguistics — parsing large corpora (like the Brown Corpus) — and how discrimant analysis (a type of regression) helps to reduce noise and expose the data that is useful.

search terms for this article:

regression, regression analysis, regression analysis in business, Applied Regression Analysis, what is regression analysis used for in business, use of regression analysis in business, linear regression in business, application of regression analysis in business, applied regression, HOW IS REGRESSION ANALYSIS USED IN BUSINESS, regression analysis examples in business, regression analysis business, regresyon, regression analysis for business, uses of regression analysis in business, importance of regression analysis in business, regression in business, regression analysis in management, what is regression analysis in business, regression analysis in healthcare, regression analysis in business decisions, regression analysis uses in business, regression analysis application in business, importance of regression analysis, regression picture, regression business, how is linear regression used in business, linear regression business, linear regression in human resources, regression analysis in human resources, examples of regression analysis in business, hr regression analysis, how does regression analysis work, business regression analysis, how regression analysis is used in business, régression, human resources regression analysis, regression analysis of a company, uses of linear regression in business, linear regression in healthcare, linear regression used in business, регрессионный анализ, регрессия, role of regression analysis in business, example of regression analysis in business, regression analysis uses business, regression analysis in HR, why use regression analysis in business, regression applied, regression analysis business example, importance of regression analysis to business organization, applications of regression in business, SIX SIGMA REGRESSION ANALYSIS, regression analysis management, linear regression business examples, regression method, what is the importance of regression analysis, regression pictures, picture of human regression, what is regression analysis, regression in business statistics, how is regression statistics used in business, linear regression in business research, Regression for business, regression in business management, use of correlation and regression in business, regression images, regression formula applied to HR, regression image, regression used by any company, importance of regression in business, regression analysis to minimize absenteeism, example regression analysis business, regression applications in business, importance of applied regression analysis, regression photo, how does regression analysis help managers, linear regression and business, regression photos, regression application in business, linear regression business analysis, regression examples, use of regression analysis in hr, why regression is used in business analysis, application of regression in toyota company, regression analysis human resources, regression analysis important business, operations management regression equation, why is regression analysis important, applications of regression analysis in businesses, regression analysis method, regression analysis example in business, uses of correlation and regression in business and management, use of regression in management, what is applied regression analysis, business regression example, business applications of regression analysis, regression analysis used in companies, regression analysis hr, regression business statistics

Related Articles: