Part of the Analyze Phase in the DMAIC Six Sigmas Methodology is to verify the potential root causes with hypothesis testing. One common hypothesis test is an application of the Chi Square Test called a Contingency Table, also called a Present / Not Present Matrix.
What is a Contingency Table
For something to be a root cause, the defect rate must be higher when root cause is present and the defect must be lower when this root cause absent. The easiest way to show this is to use 2×2 grid and look for patterns.
The data on the grid will make it very clear if what you are looking at is a root cause of the defect that you are after or not. The grid is constructed so that you have a box containing four other boxes (2×2).
On the rows, you add labels “root cause present” and “root cause absent” and across the columns, you label the columns “defect present” and “defect absent.” Then, you fill in the grid with data (numbers of observations).
You will have to go and look at some non-defective parts and see if your potential root cause is present or absent (you may already have data for your potential root cause from MEASURE, if not, you have to measure that too).
For a potential root cause to be considered verified by this tool, most of the data must be “on the diagonal.” This means that it will fall in the “defect present/root cause present” box and the “defect absent/root cause absent” box.
If it fits this pattern, then you can be confident that if you eliminate the root cause, then the defect will go away. If it does not fit this pattern, you can use more advanced Statistical Tests to verify the root causes.
As an example, let’s assume the following:
Defect: Packages in Order Fulfillment are rejected by the Packing Scanner
And, during our data collection phase in Measure, we have data that shows the data below:
|
|
|---|---|
|
|
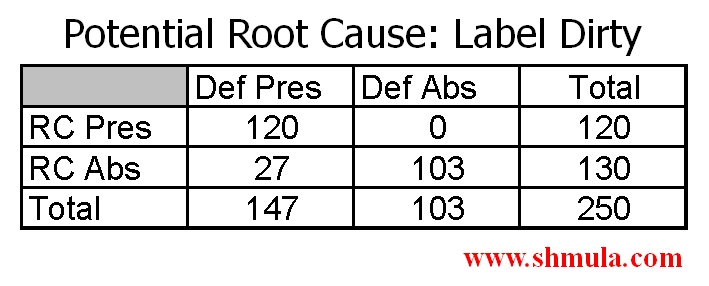
Typically, they hypothesis takes the form of:
H0: there is no relationship between dirty shipping labels and packing scanner rejections
H1: there is a relationship between dirty labels and packing scanner rejections
Given the data above, we follow this intermediate equation:
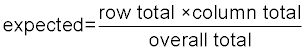
Then, we follow the Chi-Square Equation:
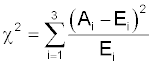
Which gives us the results below:
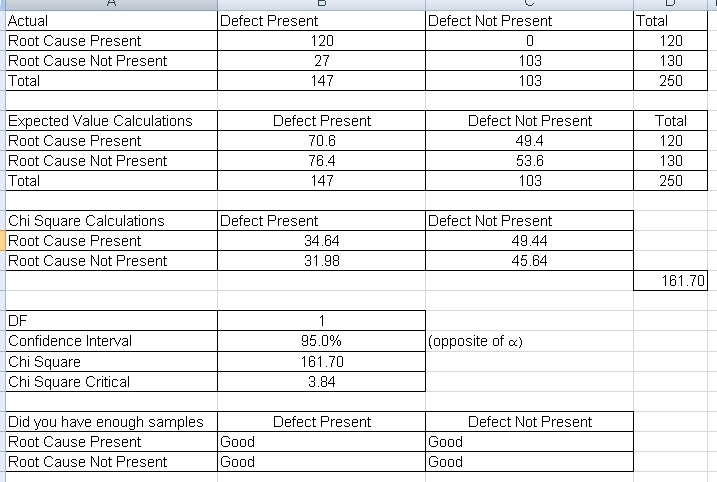
Given the results above, we can conclude the following:
We Reject the Null Hypothesis
There are many possible applications of the contingency table. Think about your business, the defects that you deal with, and perhaps there might be an opportunity to apply the Chi-Square or Contingency Table to your process.
Feel free to download a Free Chi-Square Template.
{ 0 comments… add one now }