In a previous article, I discussed the Psychology of Queueing and my experience at Disneyland while on vacation with my family. In this post, I want to briefly talk about FastPass at Disneyland, in the context of Queueing.
FastPass is a feature that Disneyland offers its customers, wherein a customer is invited to obtain a pass, redeemable only at a certain time and ends at a certain time. The idea is that during those times, theoretically, the lines will be shorter and the wait time will be shorter also. Below is a picture of what that looks like at Disneyland.
As you can see from the picture above, the customers are invited to return between 4:25PM to 5:25PM, with the idea that the wait time will be shorter. Disneyland calls this offering FastPass.

As I thought more about FastPass, I think it is a simple Queueing calculation; If I’m thinking about this correctly, then, we need to know the following items:
- λ = Arrival Rate, or more specific, the time between arrivals. For most queues, we can assume that the arrival distribution can be approximated by a Poisson distribution; which means that the time between arrivals are not deterministic, but random.
- μ = Service Rate, or more specific the time for a arrival to be serviced.
Then, Disneyland probably has historical data on when this particular ride is least congested, and I’m assuming it’s between the hours of 4:25PM and 5:25PM. Disneyland, then, can calculate, given historical congestion data and the Arrival Rate and the Service Rate, the probability of N arrivals during this 60 minute period:
(Pn = (λT)n/n!)e-λT
Where T is period T, in our Disneyland example, it is 60 minutes.
Let’s assume that Arrival Rate = 15, and we want to know the probability of 4 arrivals during this 60 minute period. Then, we get the following:
(P4 = (15*1.0)4/4!)e-15*1.0
The result of the equation above would give a % of probability of 4 arrivals during a 60 minute period.
Does FastPass Work?
I’m not sure. Our family went on plenty of rides and, on some, I saw noticed that FastPass seemed to work, whereas on others, FastPass was no faster than the regular line.
Like most things, the equations we come up with are clean and neat. But, when they meet everyday life and empirical data, things get a little muddy and much more complex.
Enough Pontificating
We had a great vacation at Disneyland. We’re already planning our next vacation — we’re thinking Hawaii. I can’t wait.
Become a Lean Six Sigma professional today!
Start your learning journey with Lean Six Sigma White Belt at NO COST


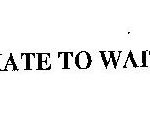



psabilla says
@Jason,
Your heijunka argument makes sense: reducing utilization is a way to manage the variability of demand.
When Disney chooses a FastPass time period, are you suggesting that they are making that decision arbitrarily, or that time period (i.e. 4:30 – 5:30) has some thought behind it? The business decisions you mention above make sense, and I wasn’t necessarily thinking of the waiting vs leisure trade-off, but it makes sense. Aside from the business reasons to have the customers roam the park, wait on another ride, I wonder how Disney decides on those FastPass time periods. Thoughts?
Pete
Jason says
I like your site, I stumbled across it a few weeks back and I’ve enjoyed the stimulating musings. I’m not sure that your thinking about fastpass correctly. I agree with your queueing calculations and that the arrival rate is poisson but I disagree that they are using historical data to shift demand to a specific period of the day.
Instead I believe they are using this to level demand and reduce variability. Wait time increases exponentially with utilization. Reduce capacity utilization and you will reduce wait time. How can Disney control this? Well they manage the heck out of capacity utilization. Capacity utilization is defined as rho = Ri/Rp, where Ri is the inflow rate and Rp is the processing rate. Therefore, they can either increase the processing rate or decrease the inflow rate.
A few words about processing rate first. Rp = c/Tp, where c is the number of servers and Tp is the processing time. They employ a number of tactics to manage both of these variables. For example, Space Mountain is actually 2 roller coasters in 1 building. This doubles their processing rate on this ride by doubling the number of servers. The processing time is composed of ride tie and load/unload time. Take Dumbo for instance. It has a fixed cycle time and simply making the right faster will eventually impact customer satisfaction (I’m sure they have experimented with the optimal ride duration). But they have ingenious staging queues to minimize load and unload procedures. What do they do? The line forks as you near the ride, each sub-line then has their own staging area that is sized for the number of seats on the ride (This has the secondary psychological effect of moving the line more often). Rides like the Pirates of the Caribbean also employ multiple staging areas as well. Finally, rides like Peter Pan and The Haunted Mansion minimize the load/unload by continually moving and having a moving walkway to enable people to load and unload without creating delay. With all this in place then Disney has turned their attention to inflow rate.
Now, back to the FastPass. Disney can’t deal with Rp by scheduling input (as might happen in a manufacturing operation) nor can they turn people away (although I think that the posted wait times may have this effect to some extent). FastPass is a demand management strategy that is primarily designed to reduce the variability of input, in a sense imposing a schedule on demand. Really what it is doing is reducing the coefficient of variation for arrival but I won’t ramble on in this direction just now. For now if we simply think of this as leveling then it is keeping the high demand peaks to a minimum. It’s not to say that they aren’t aware of traditionally high demand periods, they are and I would guess they are scheduling FastPass times based on this and on the current wait time + the number of FastPasses already issued. But on the whole, they are keeping the standard line shorter and effectively reducing utilization. But I think that capacity utilization may be the secondary benefit from FastPass.
By keeping us out of line with FastPass, Disney is making us more available to spend money. Sure FastPass results in more rides for ride enthusiasts but they limit the number of FastPasses you can have at one time. Really what can you do while your waiting for the clock to strike 4:35 so that you can ride Splash Mountain again? That’s right, buy another Micky Ice Cream pop, buy another Coke or shop in the nicely air conditioned curio off to the left.
I took my family to Disney last fall and we had a great time. I’m speculating on Disney’s motivation but these were my thoughts as I visited. They have implemented this much more effectively than Six Flags who charge for the opportunity to be managed in this way. Not great customer service but it’s tough to beat Disney in the customer service game.
Keep up the great posts!
Jason says
Pete,
Sorry I wasn’t clear on my thoughts on FP return times. I think the return time is a function of historic peak demand times as well as the current traditional line length (queue length) and the number of FP already distributed for a given return time. My experience was a FP obtained first thing in the morning would typically have an immediate window (for something like PotC or Splash Mountain). This is of relatively low value given that the line is probably short already. My daughter’s response to this was to hold the FP until the end of the window while repeatedly riding with the short line. However, for really popular rides like Everest at Animal Kingdom, a FP obtained by midmorning already had you pushed out to the late afternoon and by mid-day the FP distribution would be closed. This implied to me that this is a dynamic allocation and with a bounded number of FP slots. I would think this is due to the impact of letting FP holders essentially cut in line. There is probably a noticeable saturation point where the FP holders become generators of demand spikes which would defeat the purpose. I haven’t run any numbers but this all seems reasonable to me.
Does this answer your question?
psabilla says
@Jason,
Are you in the MIT-LFM program? I’ve spent time with Charlie Fine, the late Al Drake, Jérémie, and Theophane while I was at Amazon.
Thanks for your comments.
Pete
Chris says
Pete, Jason –
Interesting thread on Disneyland queuing strategy with FastPass. I agree with both of you that FastPass return times are determined dynamically based on historical peaks and by the number of slots that have already been filled. However, I suspect Disney’s thinking about FastPass has as much to do with customer segmentation and revenue maximization as it does with operational efficiencies.
Customers visit Disneyland with different motivations from a variety of demographic and psychographic segments. Just a few to consider: Family with 3 small children visiting from out of town for a single-day; Teenagers from Irvine with Annual Passes, visiting for one afternoon and evening; Retired couple from Nebraska on a second honeymoon; Family with three teenagers visiting for a week; Touring group of adults from Japan visiting on a 3-day pass.
Obviously, each of these groups would have different objectives in their experience, and so as Disneyland has looked to grow its attendance, it’s made new attractions, features, and promotions available to attract or keep various segments. Some customers visit Disneyland with one goal in mind: riding certain attractions. For those customers, FastPass is a good solution. It ensures that those who visit the park, sometimes from far away, and sometimes for only one day, will get to experience the hottest rides. Of course, it’s not a perfect solution, because if everybody decides to get FastPasses for the same rides at the same time, the FastPass line won’t be any shorter than the regular line (Pete mentioned that this happened to him; it’s happened to me too).
Just as importantly, as Jason rightly pointed out, getting somebody out of a line also frees them up to spend money elsewhere. In the theme park business, the goal is to maximize the combined take of admission, food & beverage, and retail during a guest’s stay.
Al says
I don’t think you guys have looked at this the right way at all, except the marketing side of Disney selling more stuff during the que time. Fast Pass times change every hour. It’s just another line to go to, but you have to have patience to come back to it. We used this on our two trips so far, especially when Test Drive first opened. We would swing by in the morning, get a pass for an hour later, go check out some other rides/venues, and then come back. When we left, we’d get another FastPass for a few hours later again.
Rode the thing 3-4 times a day, NEVER waited in line. I don’t think it has anything to do with historical data, it’s just for those who have patience. And now I hear they have another line added that you can pay extra through the Disney resorts, and not even wait in a line, or for a specific time. Just show up and skip the 300 people standing in line…
I’ll find out on Tuesday when I get down there for my third trip.
Elliott Wood says
This is an interesting discussion. We took advantage of a program called ridemax that allowed us to plan a daily itinerary based on the attractions we wanted to do. It automatically generates a schedule based on average wait times during the desired time of year and day of week, incorporating fastpasses where needed. We spent an average of 5 minutes in line for all our planned rides, minimized walking and really had little time for hanging out shopping. Disney’s House Advantage is minimized with the program.
I wonder if Disney doesn’t also take advantage of demographic information… Fastpasses are tied to your park ticket. I bought my tickets online, providing my name and address to disney. With this information, they can append my data with readily available demographic info about my age and income, likelyhood to purchase certain items,etc. They can then build a profile of the type of person that is most attracted to a certain ride or ride category, which can be used to further improve profitability by selling corporate sponsorships directed to the core ride demographic and developing attractions that cater to the most profitable segments.
May not be happening now, but the brass at disney isn’t slow…